什么是递归

递归，简单来说，就是自己调用自己，指在函数的定义中调用函数自身的方法

调用分为直接调用和间接调用，直接调用是指在函数体中调用自身，间接调用是调用别的函数，而这些别的函数又调用函数本身。它主要是把大问题变成小问题，使得代码更加简洁。理解递归需要有一定的抽象能力。

使用递归时，需要注意的是：

  • 递归就是在过程或函数里调用自身
  • 必须有一个明确的递归结束条件，称为递归出口

切勿忘记递归的出口，否则就是无限循环

著名的德罗斯特效应就是递归的一种视觉形式

递归的过程分为，递归前进段，递归边界条件，递归返回段

递归的最大层次限制是998次，但是可以通过sys(System)模块下的setrecursionlimit方法来进行递归层次的扩大

递归函数的优点是定义简单，逻辑清晰，但是，过深的调用会导致栈溢出

递归实现高斯求和

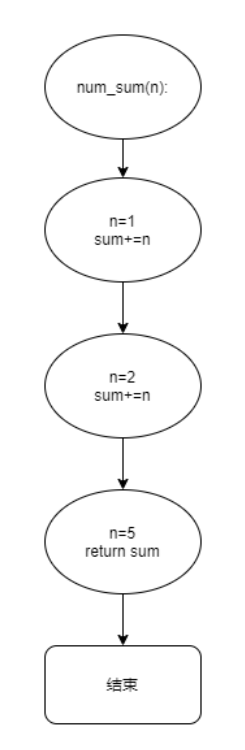
代码实现高斯求和，如果是按照正常方式实现，那么就是这样的

def sum_number(n):
    total = 0
    for i in range(1,n+1):
        total += i

    return total

非常的简单，但是这样做，流程是这样的，假设我们传参5

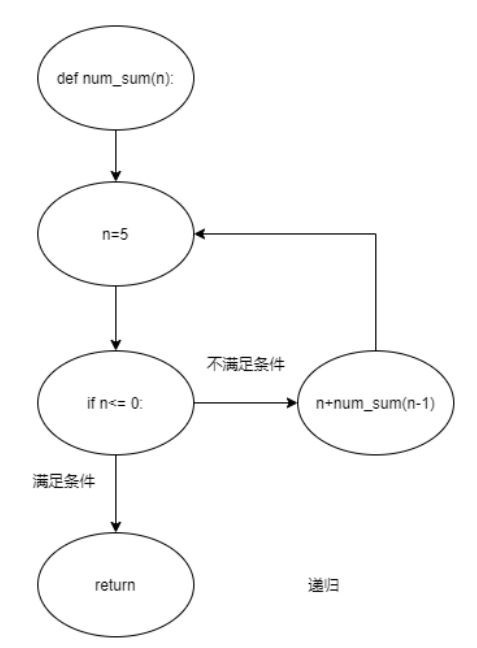
同样是计算5，我们用递归实现：

def sum_numbers(n):
    if n <= 0:
        return 0
    return n+sum_numbers(n-1)

可以看到，我们并不是从1开始加到5，而是逆向的思维，从5开始，逐渐的递减，直到边界条件触发，也就是，如果为0，则停止递归

但是，这样会造成一个后果，就是内存的耗费问题，因为递归需要同时保存成千上百个调用记录，很容易发生”栈溢出”错误（stack overflow）

尾递归

对于尾递归来说，由于只存在一个调用记录，所以永远不会发生”栈溢出”错误。

如果按照上方的递归，计算需要保存n个调用记录，复杂度为O(n)

也就是：

5 + sum_numbers(4)
5 + (4 + sum_numbers(3))
5 + (4 (3 + sum_numbers(2))
5 + (4 (3 (2 + sum_numbers(1))

在内存中，需要存储5次，非常的耗费

让我们用尾递归来实现一下，看一下有什么不同

def tail_sum(n,result=0):

    if n <= 0:
        return result
    else:
        tail_sum(n-1,result+n)

我们给定义了一个最终数result，每次调用，不再存储到内存中，而是将结果存到result中，这样，只在运行结束的瞬间，存储一次，其他时间，只是存储了状态，如下：

tail_sum(5,0)
tail_sum(4,5)
tail_sum(3,9)
tail_sum(2,12)
tail_sum(1,14)
tail_sum(0,15)

再实现一下斐波那契

def feibonacci(n):

    if n <= 2:
        return 1
    else:
        return feibonacci(n-1) + feibonacci(n-2)

总结一下， 递归最核心的思想是：每一次递归，整体问题都要比原来减小，并且递归到一定层次时，要能直接给出结果！