Jupyter Notebook

当今机器学习和数据科学从业者使用最广泛的工具是Jupyter Notebook，很多人用来编写代码、进行实验和尝试的默认环境。JupyterLab作为一种基于web的集成开发环境，你可以使用它编写notebook、操作终端、编辑markdown文本、打开交互模式、查看csv文件及图片等功能。你可以把JupyterLab当作一种究极进化版的Jupyter Notebook。原来的单兵作战，现在是海陆空联合协作。

Jupyter Notebook安装

官网，安装很简单，直接使用pip安装即可。

pip install jupyterlab

按照官网操作，安装成功后，使用jupyer lab启动服务。默认会在8888端口打开。输入http://localhost:8888就可以进入到这个环境中，看起来像是这样：

和常用的idea几乎是类似，很容易上手。

线性回归模型

监督学习中的训练集包括输入特征(例如房屋大小)和输出目标(房屋价格)，输出目标是我们将从中学习的模型的正确答案，要训练模型，需要将训练集(包括输入特征和输出目标)提供给学习算法，然后监督学习算法会产生一些功能。

我们将这个函数写成小写的f，其中f代表函数：

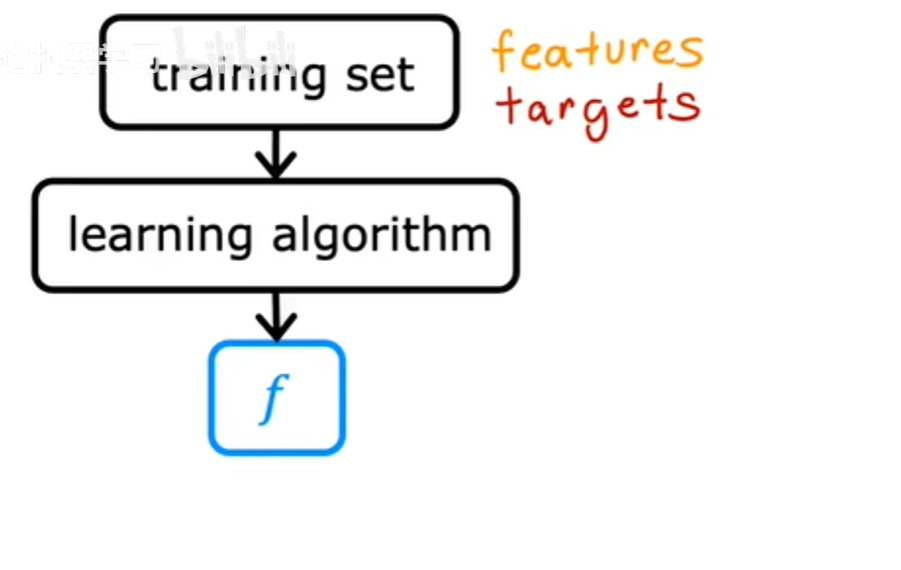
历史上，这个函数曾经被称为假设，但我在这个类中只是将它称为函数f，f的工作是采用新的输入x和输出并进行估计或预测，我将其称为y-hat，它的写法类似于顶部带有这个小帽子符号的变量y：

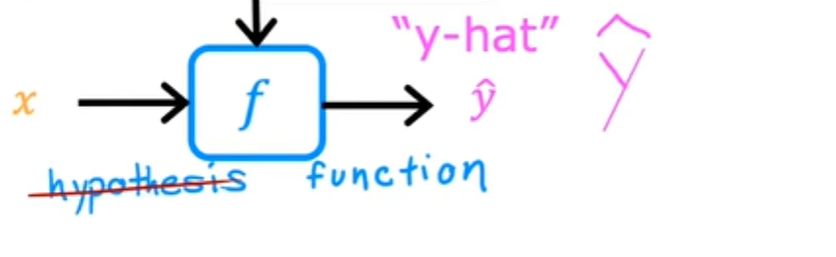
在机器学习中，惯例是，y-hat是y的估计或预测。函数f称为模型，x称为输入或输入特征，模型的输出是预测，也就是y-hat。

模型的预测是y的估计值，当符号只是字母y时，则指的是目标，即训练集中的实际真实值。相反，y-hat是一个估计值，它可能是也可能不是实际上的真实值。

参考前章节的例子，如果您正在帮助您的客户出售房子，那么在他们出售之前，房子的真实价格是未知的。您的模型f，在给定大小的情况下，输出作为估算器的价格，即对真实价格的预测。

现在，当我们设计学习算法时，一个关键问题是，我们将如何表示函数f？或者换句话说，我们要用来计算f的数学公式是什么？

现在，让我们坚持f是一条直线，你的函数可以写成f_w，x等于b，我打算用w乘以x加b。但现在，只要知道w和b是数字，为w和b选择的值将根据输入特征x确定预测y-hat，这个f_w，b of x 意味着f是一个以x作为输入的函数，并且根据w和b的值，f将输出预测y-hat的某个值，作为这个f_w，b of x的替代方法，我有时会只写f of x而没有明确地将w和b包含在下标中，只是一个更简单的符号，它的意思与f_w b of x完全相同。

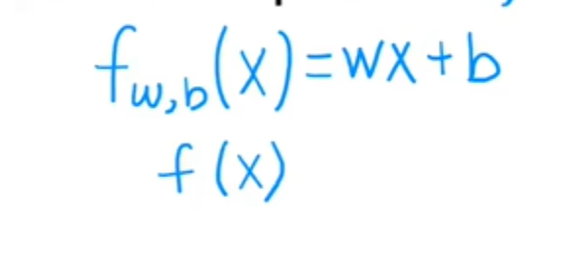
让我们在图标上绘制训练集，其中输入特征x在水平轴上，输出目标y在垂直轴上。请记住，该算法从这些数据中学习并生成最合适的线，就像这里的这条线一样。

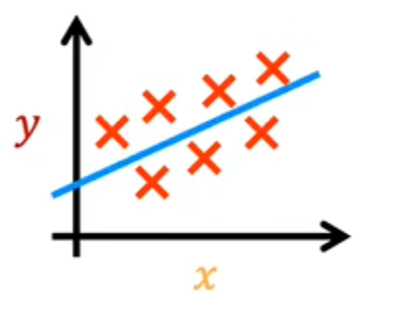
这条直线是x等于w乘以x加b的线性函数f_w b：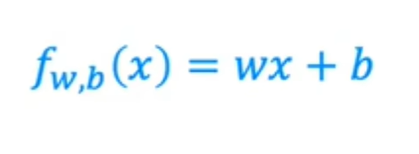

或者更简单地说，我们可以去掉w和b，只写f of x等于wx+b：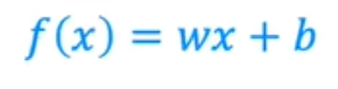

这是此函数的作用，它使用x的流线函数预测y的值。

您可能会问，为什么我们要选择线性函数，其中线性函数只是直线的一个奇特术语，而不是一些非线性函数，如曲线或抛物线。有时候也许你想拟合更复杂的非线性函数，比如这样的曲线：

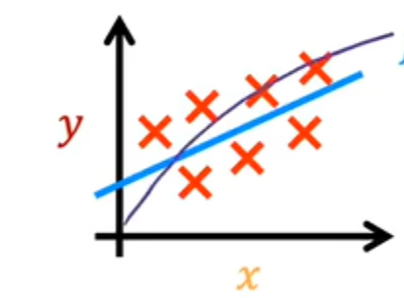
是因为由于此线性函数相对简单且易于使用，让我们使用一条线作为基础，最终将帮助您获得更复杂的非线性模型，这个特殊的模型有一个名字，叫做线性回归。更具体的说，这是具有一个变量的线性回归，其中短语”一个变量”表示只有一个输入变量x，即房屋的大小。具有一个输入变量的线性模型的另一个名称是单变量线性回归，其中uni在拉丁语中表示一个，而variate表示变量。单变量只是说一个变量的一种奇特方式。

代价函数

为了实现线性回归，第一个关键步骤是首先定义一个叫做成本函数的东西，成本函数将告诉我们模型的运行情况，以便我们可以尝试让它做得更好。

回想一下，您有一个包含输入特征x和输出目标y的训练集：

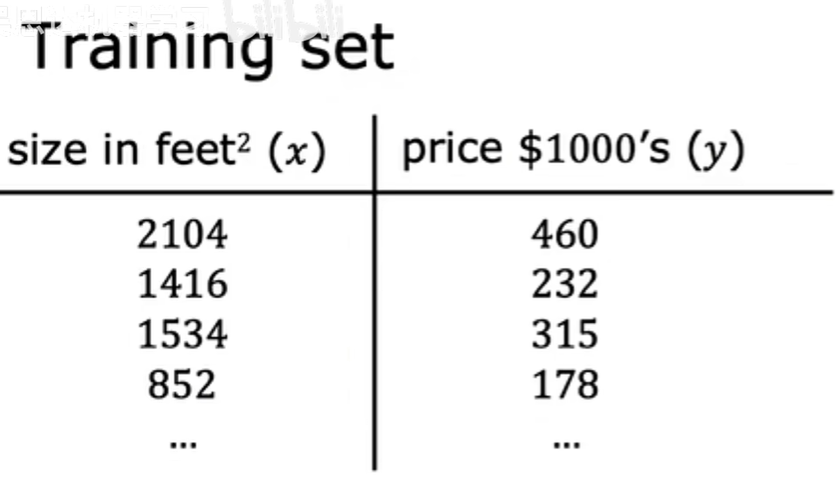
你要用来拟合这个训练集的模型是这个线性函数f_w, x of b 等于w * x+b：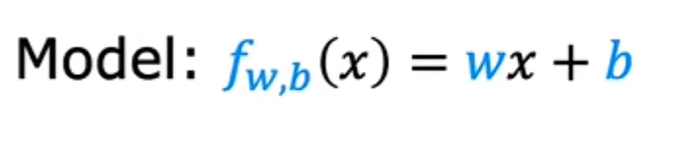

为了引入更多的术语，w和b被称为模型的参数，在机器学习中，模型的参数是您可以在训练期间调整从而改进模型的变量。这个参数w和b有时还被称为系数或权重。

根据为w和b选择的值，会得到x的不同函数f，它会在图形上生成不同的线。
当w=0,b=1.5时，f看起来就是这条横线: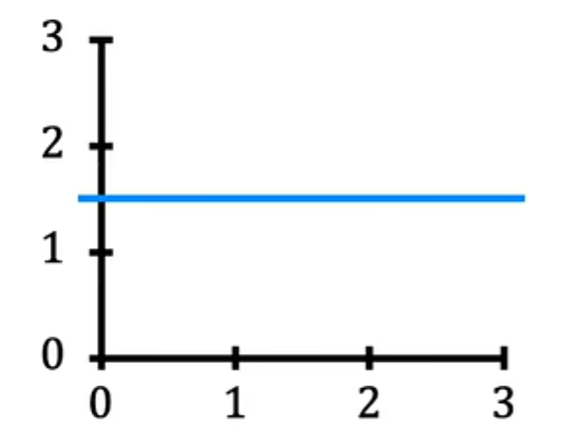

在这种情况下，x的函数f是0*x+1.5，因此f始终是一个常数值。它总是预测y的估计值为1.5，y-hat始终等于b，这里b也成为y的截距，因为这是它与垂直轴或此图上的y轴相交的地方。

如果w=0.5,b=0，则x的f为x的0.5倍，当x为0时，预测也为0，当x为2时，则预测为2的0.5倍，即1。将得到一条看起来像这样的线，并注意到斜率为0.5除以1，w的值给出了直线的斜率，即0.5：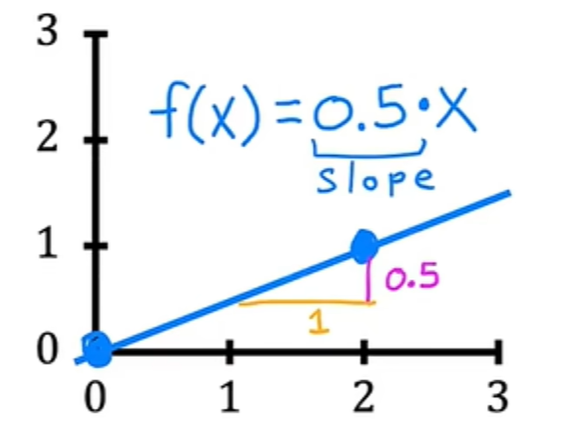

如果w=0.5,b=1则x的f是x+1的0.5倍，当x为0时，x的f等于b，即1，因此直线与垂直轴b相交，即y截距。同样的，当x为2时，x的f为2，因此该行看起来像这样：同样，这个斜率时0.5除以1，所以w的值给你的斜率为0.5：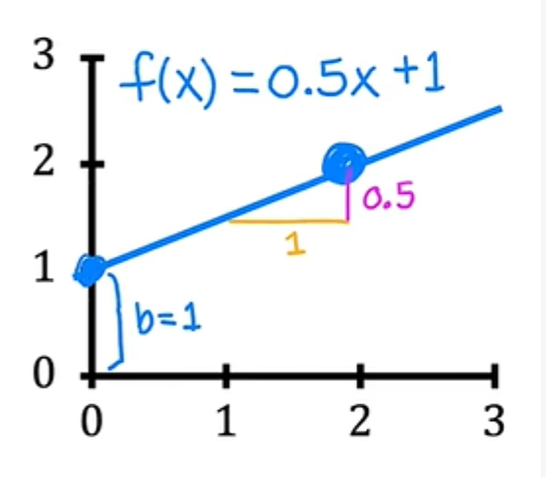

对于线性回归，您要做的时选择参数w和b的值，以便您从函数f获得的直线以某种方式很好的拟合数据。当我看到这条线在视觉上与数据相符时，你可以认为这意味着f定义的线大致穿过或接近训练示例的某个地方，而其他可能的线则不太接近这些点。ps: 只是为了提醒您一些符号，像这里这样的训练示例由x上标i,y上标i定义，其中y是目标：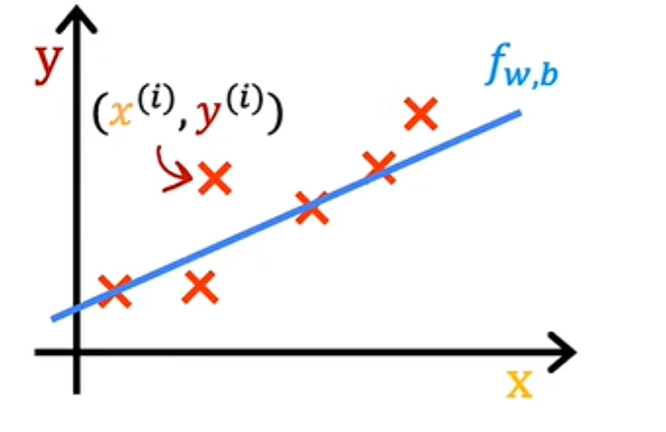

对于给定的输入x^i，函数f也为y做出预测值，并且它对y的预测值是y-hat i 在这里显示：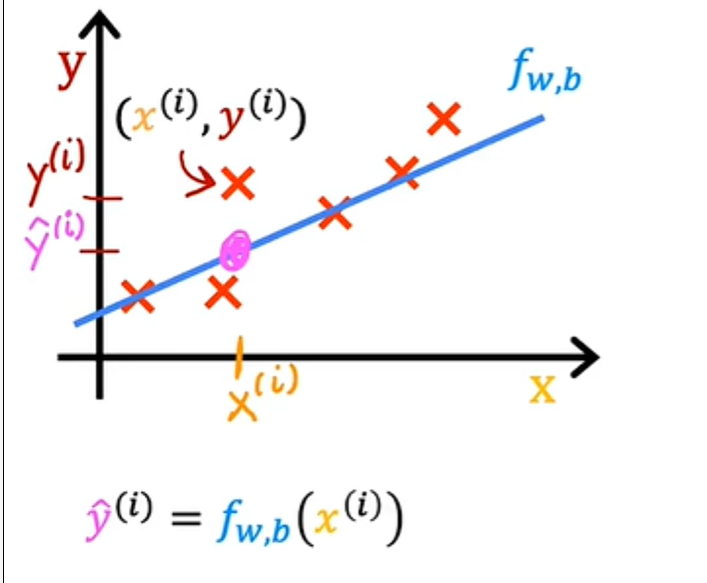

对于我们选择的x^i的模型f是w乘以x^i加上b，换句话说，预测y-hat i 是f of wb of x^i，其中对于我们使用的模型，f of x^i等于wx^i 加b：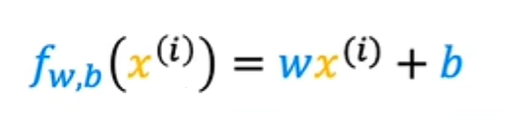

现在的问题是如何找到w和b的值，以便对于许多或可能所有训练示例x^i、y^i的预测y-hat i 接近真实目标y^i。要回答这个问题，我们先来看看如何衡量一条直线与训练数据的拟合程度，为此，我们将构建一个成本函数，成本函数采用预测y-hat并通过取y-hat减去y将其目标y进行比较。ps: (y-hat) - y，这种差异称为误差，我们正在测量预测与目标的距离。

接下来让我们计算这个误差的平方，此外，我们将要为训练集中的不同训练示例i计算此项。当测量误差时，例如i，我们将计算这个平方误差项，最后，我们要测量整个训练集的误差，特别是，让我们像这样总结平方误差，我们将从i等于1，2，3一直加到m并记住m是训练示例的数量。

按照惯例，为了构建一个不会随着训练集大小变化而自动变大的成本函数，我们将计算平均平方误差而不是总平方误差，我们通过像这样除以m来实现：。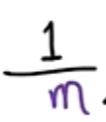

机器学习人使用的成本函数实际上是除以2乘以m，额外除以2只是为了让我们后面的一些计算看起来更整洁，但无论是否包含这个除以2，成本函数都是有效的，此处的表达式是成本函数，我们将写wb的J来指代成本函数：

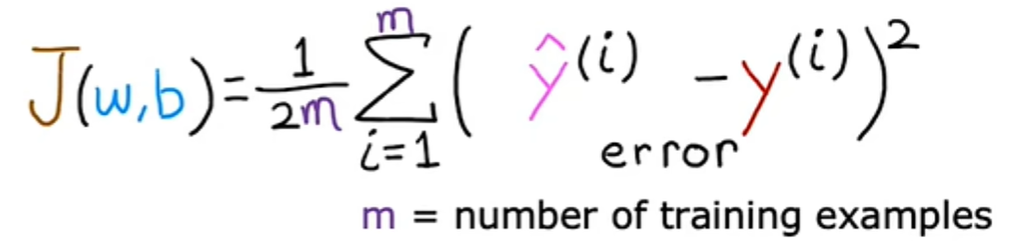
这也称为平方误差成本函数，之所以这样称呼是因为您取的是这些误差项的平方，在机器学习中，不同的人会针对不同的应用程序使用不同的成本函数，但平方误差成本函数是迄今为止线性回归最常用的函数，就此而言，对于所有回归问题，他似乎为许多应用程序提供了良好的结果。提醒一下，预测y等于模型f在x处的输出，我们可以将wb的成本函数J重写为1乘以2m乘以i等于1到m的f的x^i减去y^i的平方：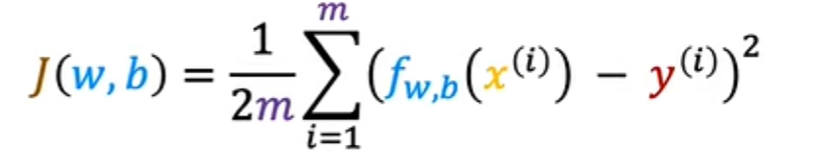

最终我们将要找到使成本函数变小的w和b的值。

todo…

暂时此系列先停止一下，因为各种原因..（好叭因为我实在我实在有太多东西不懂了，曾经学过的东西全都进行了格式化，而且很彻底，暂时停止一下，也让我补补基础，但是不允许自己停下学习的脚步，偶尔发现一个学习数学很哇塞的讲师，地址）先补补课吧，补补课再继续回归学习吴恩达老师的课程。包括之前北大肖臻老师的区块链课程，这些我曾经放弃的东西，在兜兜转转之后，发现这曾经选定的路并非不是正确的路，只是我没有好好走，仅此而已。